Hamming codes
Error correcting hamming code | |||||
| Upload media | |||||
| Instance of |
| ||||
|---|---|---|---|---|---|
| Named after |
| ||||
| |||||
parity-Bits[edit]
 |
EN: The Hamming codes are based on Parity-bits. For recapitulation this picture shows the generation of an Even-parity-bit. Hamming codes mostly are based on Even-parity-bits. To make the decision for the parity bit you have to count the 4 data bits (left). If the total number of the set data bits (black boxes) is odd you have to add a parity bit (in this picture: green box) in this line. So the nummber of bits (including the parity bit) will be even in every separate line.
DE: Hamming Codes benutzen Paritätsbits. Zur kurzen Wiederholung hier eine Tabelle, in der die Bildung eines geraden Paritätsbits dargestellt ist. Dazu wird die Anzahl der gesetzten vier Datenbits (links) gezählt. Das Paritätsbit (hier grün, rechte Spalte) wird immer dann gesetzt, wenn es erforderlich ist, um die Gesamtzahl der gesetzten Bits je Zeile gerade zu machen.
3-Bit-Hamming Code[edit]
 |
EN: The most simple and smallest Hamming code has only three bits. It is only of theoretical interest. There is one data bit (d) and two parity bits (p).
DE: Der einfachste und kürzeste Hamming-Code besteht aus nur drei Bit. Er ist nur von theoretischem Interesse. Es gibt ein Datenbit (d) und zwei Paritätsbis (p).
7-Bit-Hamming Code[edit]
 |
 |
 |
 |
EN: The teaching of the Hamming code starts with the 7-Bit-Hamming-code. But because of the big redundancy this is not applied in technical devices. Figure 1 shows the 7-Bit-Hamming-code consisting of 4 databits (d, green) and 3 parity bits (p, blue). The parity bits are on position 1, 2 and 4. dispersed between the data bits. 1, 2 and 4 are exponentiations of 2: 20, 21 and 22. Figure 2 shows almost the same as Figure 1, only that the parity bits are now positioned after the data bits. In Figure 1 the formation rule for the position of the parity bits is better visualized. Figure 3 shows the dependencies between different parity bits and data bits. Parity bit p1 (marked with a red circle and black border) is formed by checking data bits d1, d2 and d4. Parity bit p2 (marked with a green circle and black border) is formed by checking data bits d1, d3 and d4. and so forth. the Figure visualizes, that every parity bit has its own controlgroup (partially overlapping) to check some data bits. Figure 4 has the same information as Figure 3, only that the parity bits now are again dispersed between the data bits. Figure 5 to 7 visualizes again the information that is already shown in Figure 4. Figure 5 shows that parity bit p1 checks the data bits d1, d2 and d4.
DE: Der Hamming-Code wird meist mit Hilfe des 7-Bit-Hamming-Codes erklärt. Wegen seiner großen Redundanz wird er jedoch nicht technisch angewendet. Bild 1 zeigt den 7-Bit-Hamming-Code mit seinen 4 Datenbits (d, grün) und seinen 3 Paritätsbits (p, blau). Die Paritätsbits sind an den Positionen 1, 2 und 4 zwischen den Datenbits angeordnet. Das entspricht den Zweierpotenzen 0, 1 und 2. Bild 2 zeigt die gleiche Tabelle, wie Bild 1, allerdings sind hier die Paritätsbits hinter den Datenbits angeordnet. Bild 1 veranschaulicht die Bildungsvorschrift für die Positionierung der Paritätsbits besser. Bild 3 zeigt, für welche Datenbits das jeweilige Paritätsbit zuständig ist. Das Paritätsbit p1 (markiert durch einen roten Kreis mit schwarzem Rand) wird auf die Datenbis d1, d2 und d4 angewendet. Das Paritätsbit p2 (markiert durch einen grünen Kreis mi schwarzem Rand) wird auf die Datenbis d1, d3 und d4 angewendet usw. Das Bild verdeutlicht, dass die Datenbits durch verschiedene, sich teilweise überlappende Kontrollgruppen der Paritätsbits kontrolliert werden. Bild 4 enthält die gleiche Information, wie Bild 3. Allerdings sind hier wieder die Paritätsbits zwischen den Datenbits verstreut angeordnet. In Bild 5 bis 7 sind nochmals die Informationen aus Bild 4 deutlich hervorgehoben. Bild 5 zeigt, dass das Paritätsbit p1 durch Kontrolle der Datenbits d1, d2 und d4 gebildet wird. Leider ist im Bild 7 ein Fehler unterlaufen. 2. Reihe 3. Spalte und 3. Reihe 5. Spalte sind "1" Bits die dort nicht gesetzt sein sollten.
 |
 |
 |
15-Bit-Hamming Code[edit]
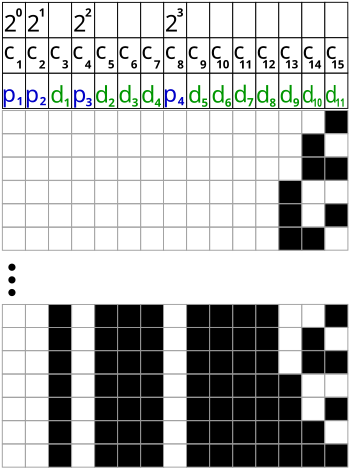
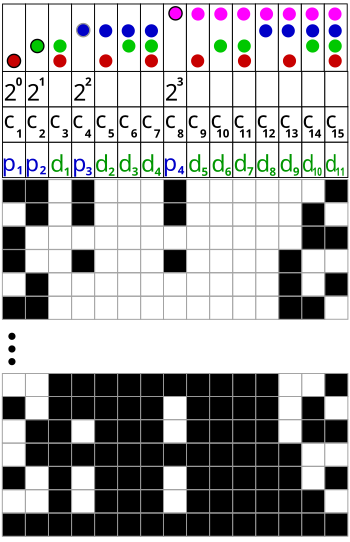
EN: The 15-Bit-Hamming-code has 11 data bits and 4 parity bits. Figure 1 shows the dispersed position of the parity bits between the data bits. the postions are: 1, 2, 4 and 8, which are the exponentiations: 20, 21, 22 and 23. Figure 2 shows which data bits is checked by which parity bit (see detailed descritption above - 3-Bit-Hamming-Code). Figure 3 shows the same information as Figure 2. The parity bits are now positioned after the data bits.
Hamming code is applicable to any kind of data blocks. In our example of the 7-Bit-Hamming-Code and of the of the 15-Bit-Hamming-Code a table of the binary digits are used. But as seen below (31-Bit-Hamming-Code) the data can also be something totally different.
 |
 |
 |
31-Bit-Hamming Code[edit]
 |