Category:Complex plane
Salti al navigilo
Salti al serĉilo
La artikolo Complex plane en Vikipedioj: - (eo) Kompleksa ebeno
- (bn) জটিল সমতল
- (de) Komplexe Ebene
- (en) Complex plane
- (es) Plano complejo
- (fa) صفحه مختلط
- (fr) Plan complexe
- (he) המישור המרוכב
- (it) Piano complesso
- (ja) 複素数#ガウス平面
- (nl) Complexe vlak
- (pl) Płaszczyzna zespolona
- (pt) Plano complexo
- (sr) Комплексна раван
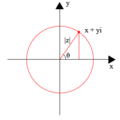
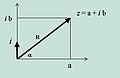
geometric representation of the complex numbers  | |||||
| Alŝuti plurmedion | |||||
| Estas |
| ||||
|---|---|---|---|---|---|
| Subaro de | |||||
| |||||
 | |||||
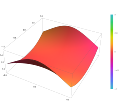
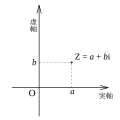
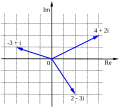
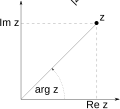
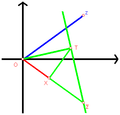
English: The complex plane in mathematics, is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis.
Subkategorioj
Ĉi tiu kategorio havas la 4 jenajn subkategoriojn, el 4 entute.
C
- Complex conjugation (23 D)
- Complex multiplication (24 D)
U
- Unit circles - complex plane (12 D)
Dosieroj en kategorio “Complex plane”
La jenaj 200 dosieroj estas en ĉi tiu kategorio, el 281 entute.
(antaŭa paĝo) (sekva paĝo)-
-z.png 541 × 523; 21 KB
-
040324 ktm 10.png 91 × 91; 359 bajtoj
-
2z.png 624 × 561; 18 KB
-
3rd roots of unity on the complex plane.svg 400 × 400; 20 KB
-
3rd roots of unity.jpg 400 × 400; 8 KB
-
90-Degree Rotations in the Complex Plane.png 380 × 362; 17 KB
-
90-Degree Rotations in the Complex Plane.svg 200 × 200; 1 KB
-
-
-
-
-
-
-
A plus bi.svg 182 × 122; 1 KB
-
-
Affixe vecteur.svg 1 830 × 1 470; 25 KB
-
Affixe.svg 514 × 433; 17 KB
-
Algebraic integers in the complex plane.png 790 × 489; 261 KB
-
Algebraic integers.gif 1 404 × 1 404; 279 KB
-
Algebraic number in the complex plane.png 779 × 516; 315 KB
-
Argand 2.svg 233 × 144; 25 KB
-
Argand 3.svg 223 × 282; 37 KB
-
Argand 4.svg 175 × 259; 38 KB
-
Argand 5.svg 175 × 259; 37 KB
-
Argand-2.png 787 × 782; 51 KB
-
Argand.png 589 × 504; 10 KB
-
Argand2.png 300 × 300; 4 KB
-
Arganddiagram.png 765 × 917; 33 KB
-
Argandgaussplane.png 300 × 300; 4 KB
-
Argument of a complex number.svg 531 × 341; 11 KB
-
Argument.PNG 254 × 167; 2 KB
-
Argumentfunktion.png 800 × 800; 37 KB
-
Argumentfunktion2.png 800 × 800; 37 KB
-
Arguments sum.svg 709 × 583; 38 KB
-
Auswirkung Polpunktlage Systemfunktion.svg 928 × 716; 27 KB
-
Bilinear transform phase diagram.png 924 × 478; 4 KB
-
Bilinear transform s-z-plane.png 1 237 × 1 667; 41 KB
-
Bilinear transform s-z-plane.svg 470 × 690; 60 KB
-
Bin-imaginary 5+3i.svg 600 × 600; 6 KB
-
Cayley transform in complex plane.png 1 188 × 840; 68 KB
-
Cmplxpower.svg 793 × 499; 22 KB
-
Compl 01.gif 822 × 90; 3 KB
-
Compl 02.gif 830 × 112; 3 KB
-
Compl 03.gif 832 × 403; 3 KB
-
Compl 04.gif 827 × 401; 3 KB
-
Compl 05.gif 844 × 407; 4 KB
-
Compl 06.gif 827 × 401; 4 KB
-
Compl 07.gif 832 × 403; 3 KB
-
Compl 08.gif 832 × 403; 3 KB
-
Compl 09.gif 832 × 403; 3 KB
-
Compl 1.gif 822 × 90; 2 KB
-
Compl 10.gif 827 × 401; 4 KB
-
Compl 11.gif 827 × 401; 4 KB
-
Compl 12.gif 827 × 401; 4 KB
-
Compl 13.gif 827 × 401; 5 KB
-
Compl 14.gif 827 × 401; 4 KB
-
Compl 15.gif 452 × 401; 4 KB
-
Compl 16.gif 451 × 401; 4 KB
-
Compl 17.gif 451 × 401; 4 KB
-
Compl 18.gif 451 × 401; 4 KB
-
Compl 2.gif 830 × 112; 3 KB
-
Compl 3.gif 832 × 403; 4 KB
-
Compl 4.gif 827 × 401; 5 KB
-
Compl 5.gif 844 × 407; 5 KB
-
Complejog1.png 341 × 206; 5 KB
-
Complesso.png 200 × 300; 3 KB
-
Complex a b.PNG 319 × 241; 5 KB
-
Complex getal cartesisch.png 150 × 150; 1 KB
-
Complex getal poolcoördinaten.png 621 × 556; 16 KB
-
Complex getal.png 720 × 540; 2 KB
-
Complex mandelbrot illustration.png 2 000 × 1 780; 885 KB
-
Complex mandelbrot illustration.svg 142 × 126; 1,19 MB
-
Complex mapping.jpg 567 × 321; 25 KB
-
Complex mapping.svg 531 × 301; 15 KB
-
Complex modulus - English version.svg 920 × 320; 11 KB
-
Complex modulus - French version.svg 1 002 × 320; 11 KB
-
Complex modulus.gif 562 × 197; 3 KB
-
Complex multi.svg 700 × 600; 3 KB
-
Complex multiplication.svg 500 × 300; 20 KB
-
Complex number illustration modarg.png 180 × 202; 9 KB
-
Complex number illustration modarg.svg 180 × 180; 5 KB
-
Complex number illustration multiarg.svg 152 × 158; 14 KB
-
Complex number illustration multiple arguments.svg 204 × 217; 25 KB
-
Complex number illustration.png 180 × 132; 5 KB
-
Complex number illustration.svg 180 × 180; 1 KB
-
Complex Number.png 485 × 436; 15 KB
-
Complex number.svg 726 × 657; 21 KB
-
Complex Number2.png 360 × 360; 7 KB
-
Complex numbers addition.png 468 × 473; 16 KB
-
Complex numbers addition.svg 512 × 516; 3 KB
-
Complex numbers imaginary unit.svg 702 × 643; 20 KB
-
Complex numbers intheplane.svg 218 × 215; 34 KB
-
Complex picture.svg 240 × 240; 50 KB
-
Complex plane basic example.svg 512 × 512; 4 KB
-
Complex plane cartesian.svg 512 × 512; 4 KB
-
Complex plane diagram japanese.svg 200 × 200; 20 KB
-
Complex plane examples 1.svg 512 × 512; 7 KB
-
Complex plane malayalam.png 429 × 394; 6 KB
-
Complex Plane number -2 by rotation of 2i by 90 degrees.svg 512 × 467; 5 KB
-
Complex Plane number -2i by rotation of -2 by 90 degrees.svg 512 × 467; 5 KB
-
Complex Plane number -i by rotation 1 by -90 degrees.svg 512 × 467; 7 KB
-
Complex Plane number 2i by rotation 2 by 90 degrees.svg 512 × 467; 5 KB
-
Complex Plane number i and 1.svg 512 × 467; 6 KB
-
Complex Plane number i by rotation 1 by -90 degrees.svg 512 × 467; 7 KB
-
Complex Plane number i by rotation 1 by 90 degrees.svg 512 × 467; 6 KB
-
Complex plane polar coord.svg 512 × 512; 3 KB
-
Complex Plane.png 483 × 421; 17 KB
-
Complex sequence 1 Z2.webm 12 s, 1 280 × 720; 3,05 MB
-
Complex sequence.webm 13 s, 1 280 × 720; 3,05 MB
-
Complex sqrt leaf1.jpg 641 × 641; 92 KB
-
Complex sqrt leaf2.jpg 649 × 649; 93 KB
-
Complex vector.jpg 270 × 294; 21 KB
-
Complex vector.svg 832 × 754; 18 KB
-
Complex vlak.png 400 × 400; 2 KB
-
Complex-number-representation.png 540 × 520; 37 KB
-
Complex.png 200 × 300; 3 KB
-
Complex4.png 1 578 × 1 005; 19 KB
-
ComplexaTalplanet-2.svg 380 × 342; 15 KB
-
ComplexaTalplanet.png 800 × 862; 45 KB
-
Complexes.svg 512 × 463; 1 KB
-
ComplexMultiplication.png 718 × 659; 5 KB
-
Complexnumber.png 1 542 × 1 005; 17 KB
-
Complexnumbers.png 694 × 442; 41 KB
-
Complexo.png 741 × 521; 25 KB
-
Complexos 2.PNG 703 × 587; 20 KB
-
Complexos 3.PNG 697 × 570; 17 KB
-
Complexos.png 568 × 530; 18 KB
-
ComplexPlane Number 2 by multiplying -2i by i.svg 512 × 467; 5 KB
-
ComplexPlane Number2.svg 512 × 467; 4 KB
-
ComplexPlane Number2i.svg 510 × 510; 6 KB
-
Complexplane.JPG 286 × 304; 7 KB
-
ComplexPlane.png 228 × 289; 1 KB
-
ComplexVector2.jpg 280 × 282; 20 KB
-
Costruzione inverso complesso01.png 335 × 360; 5 KB
-
Costruzione inverso complesso02.png 360 × 345; 6 KB
-
DBP 1977 928 Carl Friedrich Gauß.jpg 670 × 1 070; 477 KB
-
Depicting complex numbers.JPG 353 × 228; 6 KB
-
Diagram of Argand (Wessel).svg 718 × 683; 18 KB
-
Discrete complex vector components.svg 210 × 202; 19 KB
-
DritteWurzelAusZ V2.jpg 570 × 558; 67 KB
-
Eixo complexo 02.svg 480 × 326; 14 KB
-
Exponential map of the sphere.svg 470 × 400; 24 KB
-
Exponentials of complex number within unit circle-2.svg 591 × 590; 39 KB
-
Exponentials of complex number within unit circle.svg 591 × 590; 25 KB
-
ExponentielleComplexe CarréComplexe.png 387 × 233; 18 KB
-
ExponentielleComplexe Conjugué.png 283 × 350; 18 KB
-
ExponentielleComplexe DivisionComplexe.png 307 × 232; 18 KB
-
ExponentielleComplexe InverseComplexe.png 352 × 363; 22 KB
-
ExponentielleComplexe MultiplicationComplexe.png 310 × 203; 18 KB
-
ExponentielleComplexe Oppose2.png 301 × 296; 21 KB
-
ExponentielleComplexe Puissances2.png 320 × 322; 24 KB
-
ExponentielleComplexe ValeursParticulieres.png 300 × 302; 17 KB
-
ExponentielleComplexe ValeursParticulieres2.png 298 × 300; 17 KB
-
F(t)=(1+i)t.gif 368 × 396; 306 KB
-
F(t)=-t.gif 368 × 396; 265 KB
-
F(t)=3%(t-i).gif 368 × 396; 344 KB
-
F(t)=exp((-1%3+2i)t).gif 368 × 396; 697 KB
-
F(t)=exp(2it)+t.gif 368 × 396; 454 KB
-
F(t)=exp(it)+cos(t).gif 368 × 396; 356 KB
-
F(t)=exp(it).gif 368 × 396; 317 KB
-
F(t)=it.gif 368 × 396; 300 KB
-
F(t)=t%2.gif 368 × 396; 263 KB
-
F(t)=t.gif 368 × 396; 263 KB
-
F(t)=t^2%5.gif 368 × 396; 273 KB
-
Feigenbaum stretch.png 1 500 × 500; 668 KB
-
-
Gauss'sche Ebene und Beispiele.svg 829 × 673; 37 KB
-
Gaussian integer lattice.png 434 × 319; 6 KB
-
GaussZ3.PNG 432 × 305; 4 KB
-
Gauß'sche Zahlenebene.svg 1 946 × 1 558; 87 KB
-
Gaußsche Zahlenebene2.svg 1 071 × 857; 91 KB
-
Gaußsche Zahlenebene3.svg 1 318 × 1 030; 54 KB
-
Imaginary2Root.svg 480 × 480; 3 KB
-
Imaginary3Root.svg 480 × 480; 3 KB
-
Imaginarynumber.PNG 323 × 423; 8 KB
-
Imaginarynumber2.PNG 265 × 220; 4 KB
-
ImaginaryUnit5.png 500 × 480; 4 KB
-
ImaginaryUnit5.svg 480 × 480; 2 KB
-
ImagMulDiv3.jpg 322 × 366; 40 KB
-
Jordan lemma-complex path.png 594 × 384; 20 KB
-
Jordan's Lemma.svg 600 × 300; 27 KB
-
Joukowsky transform.svg 512 × 384; 18 KB
-
Jouktrans.png 483 × 374; 10 KB
-
Karman Trefftz transform.svg 512 × 384; 43 KB
-
Komplexe zeiger.png 300 × 300; 5 KB
-
Komplexni rovina.png 256 × 256; 3 KB
-
Komplexni-cesta-1.png 615 × 509; 28 KB
-
Komplexni-cesta-2.png 644 × 469; 19 KB
-
Komplexni-cesta-4.png 610 × 430; 14 KB
-
KomplextAbsolutbelopp.svg 261 × 231; 9 KB
-
LogGamma Analytic Function.png 900 × 600; 108 KB
-
MA2PoleZero C.svg 313 × 286; 45 KB
-
Matched Z-Transformation s-z-plane.svg 470 × 690; 26 KB
-
Meio z.png 616 × 569; 18 KB
-
Module of a complex number.svg 531 × 341; 10 KB
-
Modulus and argument.png 300 × 300; 4 KB
-
Multiplication complexes.png 287 × 220; 3 KB
-
Multiplication gives a 45 degree rotation.png 276 × 191; 8 KB
-
MultiplicationComplexes.png 790 × 523; 20 KB
-
Multiplying.png 245 × 188; 8 KB
_in_the_complex_plane_from_-2-2i_to_2%2B2i_with_colors_created_with_the_Mathematica_function_ComplexPlot3D.svg)
_in_the_complex_plane_from_-2-2i_to_2%2B2i_with_colors_created_with_the_Mathematica_function_ComplexPlot3D.svg)
_in_the_complex_plane_from_-2-2i_to_2%2B2i_with_colors_created_with_the_Mathematica_function_ComplexPlot3D.svg)
_in_the_complex_plane_from_-2-2i_to_2%2B2i_with_colors_created_with_the_Mathematica_function_ComplexPlot3D.svg)
_in_the_complex_plane_from_-2-2i_to_2%2B2i_with_colors_created_with_the_Mathematica_function_ComplexPlot3D.svg)
_in_the_complex_plane_from_-2-2i_to_2%2B2i_with_colors_created_with_the_Mathematica_function_ComplexPlot3D.svg)
.svg)
%3D(1%2Bi)t.gif)
%3D-t.gif)
%3D3%25(t-i).gif)
%3Dexp((-1%253%2B2i)t).gif)
%3Dexp(2it)%2Bt.gif)
%3Dexp(it)%2Bcos(t).gif)
%3Dexp(it).gif)
%3Dit.gif)
%3Dt%252.gif)
%3Dt.gif)
%3Dt%5E2%255.gif)
