File:DiffusionMicroMacro.gif
维基共享资源,媒体文件资料库
跳转到导航
跳转到搜索
DiffusionMicroMacro.gif (360 × 300像素,文件大小:402 KB,MIME类型:image/gif、循环、60帧、6.5秒)
文件信息
结构化数据
说明
说明
添加一行文字以描述该文件所表现的内容
ব্যাপন প্রক্রিয়া

|
File:DiffusionMicroMacro.svg是此文件的矢量版本。 如果此文件质量不低于原点阵图,就应该将这个GIF格式文件替换为此文件。
File:DiffusionMicroMacro.gif → File:DiffusionMicroMacro.svg
更多信息请参阅Help:SVG/zh。
|
摘要
[编辑]| 描述DiffusionMicroMacro.gif |
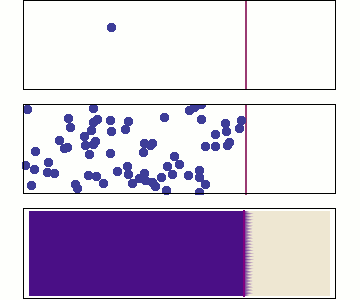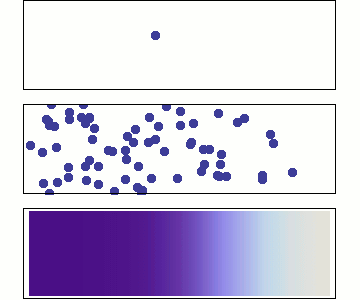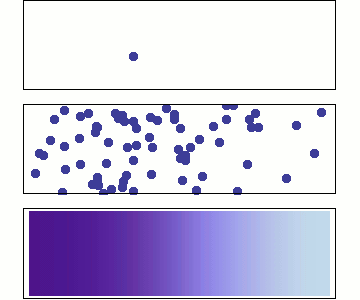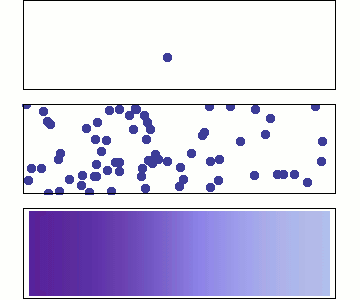
English: Diffusion from a microscopic and macroscopic point of view. Initially, there are solute molecules on the left side of a barrier (magenta line) and none on the right. The barrier is removed, and the solute diffuses to fill the whole container. Top: A single molecule moves around randomly. Middle: With more molecules, there is a clear trend where the solute fills the container more and more evenly. Bottom: With an enormous number of solute molecules, the randomness is gone: The solute appears to move smoothly and systematically from high-concentration areas to low-concentration areas, following Fick's laws.
Image is made in Mathematica, source code below. |
| 日期 | |
| 来源 | 自己的作品 |
| 作者 | Sbyrnes321 |
许可协议
[编辑]| Public domainPublic domainfalsefalse |
| 我,本作品著作权人,释出本作品至公有领域。这适用于全世界。 在一些国家这可能不合法;如果是这样的话,那么: 我无条件地授予任何人以任何目的使用本作品的权利,除非这些条件是法律规定所必需的。 |
<< Mathematica source code >>
(* Source code written in Mathematica 6.0, by Steve Byrnes, 2010.
I release this code into the public domain. Sorry it's messy...email me any questions. *)
(*Particle simulation*)
SeedRandom[1];
NumParticles = 70;
xMax = 0.7;
yMax = 0.2;
xStartMax = 0.5;
StepDist = 0.04;
InitParticleCoordinates = Table[{RandomReal[{0, xStartMax}], RandomReal[{0, yMax}]}, {i, 1, NumParticles}];
StayInBoxX[x_] := If[x < 0, -x, If[x > xMax, 2 xMax - x, x]];
StayInBoxY[y_] := If[y < 0, -y, If[y > yMax, 2 yMax - y, y]];
StayInBoxXY[xy_] := {StayInBoxX[xy[[1]]], StayInBoxY[xy[[2]]]};
StayInBarX[x_] := If[x < 0, -x, If[x > xStartMax, 2 xStartMax - x, x]];
StayInBarY[y_] := If[y < 0, -y, If[y > yMax, 2 yMax - y, y]];
StayInBarXY[xy_] := {StayInBarX[xy[[1]]], StayInBarY[xy[[2]]]};
MoveAStep[xy_] := StayInBoxXY[xy + {RandomReal[{-StepDist, StepDist}], RandomReal[{-StepDist, StepDist}]}];
MoveAStepBar[xy_] := StayInBarXY[xy + {RandomReal[{-StepDist, StepDist}], RandomReal[{-StepDist, StepDist}]}];
NextParticleCoordinates[ParticleCoords_] := MoveAStep /@ ParticleCoords;
NextParticleCoordinatesBar[ParticleCoords_] := MoveAStepBar /@ ParticleCoords;
NumFramesBarrier = 10;
NumFramesNoBarrier = 50;
NumFrames = NumFramesBarrier + NumFramesNoBarrier;
ParticleCoordinatesTable = Table[0, {i, 1, NumFrames}];
ParticleCoordinatesTable[[1]] = InitParticleCoordinates;
For[i = 2, i <= NumFrames, i++,
If[i <= NumFramesBarrier,
ParticleCoordinatesTable[[i]] = NextParticleCoordinatesBar[ParticleCoordinatesTable[[i - 1]]],
ParticleCoordinatesTable[[i]] = NextParticleCoordinates[ParticleCoordinatesTable[[i - 1]]]];];
(*Plot full particle simulation*)
makeplotbar[ParticleCoord_] :=
ListPlot[{ParticleCoord, {{xStartMax, 0}, {xStartMax, yMax}}}, Frame -> True, Axes -> False,
PlotRange -> {{0, xMax}, {0, yMax}}, Joined -> {False, True}, PlotStyle -> {PointSize[.03], Thick},
AspectRatio -> yMax/xMax, FrameTicks -> None];
makeplot[ParticleCoord_] :=
ListPlot[ParticleCoord, Frame -> True, Axes -> False, PlotRange -> {{0, xMax}, {0, yMax}}, Joined -> False,
PlotStyle -> PointSize[.03], AspectRatio -> yMax/xMax, FrameTicks -> None]
ParticlesPlots =
Join[Table[makeplotbar[ParticleCoordinatesTable[[i]]], {i, 1, NumFramesBarrier}],
Table[makeplot[ParticleCoordinatesTable[[i]]], {i, NumFramesBarrier + 1, NumFrames}]];
(*Plot just the first particle in the list...Actually the fifth particle looks better. *)
FirstParticleTable = {#[[5]]} & /@ ParticleCoordinatesTable;
FirstParticlePlots =
Join[Table[makeplotbar[FirstParticleTable[[i]]], {i, 1, NumFramesBarrier}],
Table[makeplot[FirstParticleTable[[i]]], {i, NumFramesBarrier + 1, NumFrames}]];
(* Continuum solution *)
(* I can use the simple diffusion-on-an-infinite-line formula, as long as I correctly periodically replicate the
initial condition. Actually just computed nearest five replicas in each direction, that was a fine approximation. *)
(* k = diffusion coefficient, visually matched to simulation. *)
k = .0007;
u[x_, t_] := If[t == 0, If[x <= xStartMax, 1, 0], 1/2 Sum[
Erf[(x - (-xStartMax + 2 n xMax))/Sqrt[4 k t]] - Erf[(x - (xStartMax + 2 n xMax))/Sqrt[4 k t]], {n, -5, 5}]];
ContinuumPlots = Join[
Table[Show[
DensityPlot[1 - u[x, 0], {x, 0, xMax}, {y, 0, yMax},
ColorFunctionScaling -> False, AspectRatio -> yMax/xMax,
FrameTicks -> None],
ListPlot[{{xStartMax, 0}, {xStartMax, yMax}}, Joined -> True,
PlotStyle -> {Thick, Purple}]],
{i, 1, NumFramesBarrier}],
Table[
DensityPlot[1 - u[x, tt], {x, 0, xMax}, {y, 0, yMax},
ColorFunctionScaling -> False, AspectRatio -> yMax/xMax,
FrameTicks -> None],
{tt, 1, NumFramesNoBarrier}]];
(*Combine and export *)
TogetherPlots =
Table[GraphicsGrid[{{FirstParticlePlots[[i]]}, {ParticlesPlots[[i]]}, {ContinuumPlots[[i]]}},
Spacings -> Scaled[0.2]], {i, 1, NumFrames}];
Export["test.gif", Join[TogetherPlots, Table[Graphics[], {i, 1, 5}]],
"DisplayDurations" -> {10}, "AnimationRepititions" -> Infinity ]
文件历史
点击某个日期/时间查看对应时刻的文件。
| 日期/时间 | 缩略图 | 大小 | 用户 | 备注 | |
|---|---|---|---|---|---|
| 当前 | 2012年3月7日 (三) 13:41 |  | 360 × 300(402 KB) | Dratini0(留言 | 贡献) | Just removed the white last fram for aesthetic purposes, and prologed the display time of the last frame to mark the reatart of the animation. |
| 2010年3月25日 (四) 19:37 |  | 360 × 300(402 KB) | Aiyizo(留言 | 贡献) | Optimized animation, converted to 256 color mode | |
| 2010年1月16日 (六) 09:57 |  | 360 × 300(529 KB) | Sbyrnes321(留言 | 贡献) | sped up bottom panel to match better with middle panel | |
| 2010年1月16日 (六) 09:46 | 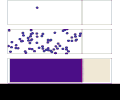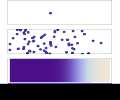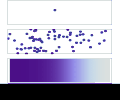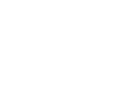 | 360 × 300(508 KB) | Sbyrnes321(留言 | 贡献) | {{Information |Description={{en|1=Diffusion from a microscopic and macroscopic point of view. Initially, there are solute molecules on the left side of a barrier (purple line) and none on the right. The barrier is removed, and the solute diffuses to fill |
您不可以覆盖此文件。
文件用途
以下页面使用本文件:
全域文件用途
以下其他wiki使用此文件:
- ar.wikipedia.org上的用途
- ast.wikipedia.org上的用途
- bn.wikipedia.org上的用途
- ca.wikipedia.org上的用途
- cy.wikipedia.org上的用途
- el.wikipedia.org上的用途
- en.wikipedia.org上的用途
- es.wikipedia.org上的用途
- et.wikipedia.org上的用途
- fa.wikipedia.org上的用途
- fi.wikipedia.org上的用途
- fr.wikipedia.org上的用途
- ga.wikipedia.org上的用途
- gl.wikipedia.org上的用途
- he.wikipedia.org上的用途
- hi.wikipedia.org上的用途
- is.wikipedia.org上的用途
- kk.wikipedia.org上的用途
- ko.wikipedia.org上的用途
- no.wikipedia.org上的用途
- pl.wikipedia.org上的用途
- pt.wikipedia.org上的用途
- ro.wikipedia.org上的用途
- sh.wikipedia.org上的用途
- sk.wikipedia.org上的用途
- sl.wikipedia.org上的用途
- sr.wikipedia.org上的用途
- ta.wikipedia.org上的用途
- uk.wikipedia.org上的用途
查看此文件的更多全域用途。