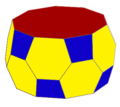
Conway polyhedra
Conway polyhedra are polyhedra made by applying en:Conway polyhedron operations. Iterating operators on simple forms can produce progressively larger polyhedra, maintaining the fundamental symmetry of the seed element.
Groups of Symmetry[edit]
All of the solids and planar tilings below have point groups (as well as global rotation and translation groups, respectively), which are one of the following forms:
These are the dihedral groups of order 3, 4, 5, 6, and are formed by the semidirect product of incremental rotations and reflections. So by means of . [1] Each right triangle is a fundamental domain which can be mapped to any other right triangle.
Tetrahedral symmetry[edit]
-
tatT
-
stT
-
XT (10e)
-
dXT (10e)
-
m3T
-
b3T
Octahedral symmetry[edit]
-
daC (2e)
-
cO (4e)
-
dakC (6e)
-
m3C (6e)
-
m3O (6e)
-
b3C (6e)
-
b3O (6e)
-
atC (6e)
-
qC (6e)
-
edaC (8e)
-
dktO=tkC (9e)
-
XO (10e)
-
XC (10e)
-
dXO (10e)
-
dXC (10e)
-
L0C
-
cdkC (12e)
-
ccC (16e)
-
tkdkC (18e)
-
tatO (18e)
-
tatC (18e)
-
l6l8taC (22e)
-
ccdkC (48e)
-
wrwC (49e)
-
cccC (64e)
-
tktkC (81e)
- Chiral
Icosahedral symmetry[edit]
-
kD = daD (2e)
-
cI (4e) *
-
atD (6e)
-
qD (6e)
-
m3D (6e)
-
m3I (6e)
-
b3D (6e)
-
b3I (6e)
-
edaD (8e) *
-
tkdD (9e) *
-
gaD (10e) *
-
XI (10e)
-
XD (10e)
-
dXI (10e)
-
dXD (10e)
-
cdkD (12e)
-
m3aI (12e)
-
tatI = takD (18e)
-
tatD (18e)
-
atkD (18e)
-
m3tD (18e)
-
qtI = t5t6otI (18e)
-
dqtI = k5k6etI (18e)
-
actI (24e)
-
kdktI (27e)
-
tktI (27e)
-
dctkD (36e)
-
ctkD (36e)
- Chiral
-
dsD (5e)
-
sD (5e)
-
wD (7e)
-
k5sD (7e)
-
saD (10e)
-
saD (10e)
-
g3D (11e)
-
s3D (11e)
-
g3I (11e)
-
s3I (11e)
-
stI (15e)
-
stD (15e)
-
wtI (21e)
-
k5k6stI (21e)
Dihedral symmetry[edit]
-
t4daA4=cA4
-
t4daA4=cA4 (side)
-
t4daA4=cA4 (top)
-
tA4
-
tA5
-
eP3 = aaP3
-
eA4 = aaA4
Toroidal symmetry[edit]
Torioidal tilings exist on the flat torus on the surface of a duocylinder in four dimensions but can be projected down to three dimensions as an ordinary torus. These tilings are topologically similar subsets of the Euclidean plane tilings.
-
A 1x1 regular square torus, {4,4}1,0
-
A regular 4x4 square torus, {4,4}4,0
-
tQ24×12 projected to torus
-
taQ24×12 projected to torus
-
actQ24×8 projected to torus
-
tH24×12 projected to torus
-
taH24×8 projected to torus
-
kH24×12 projected to torus
Euclidean square symmetry[edit]
-
tQ
-
cQ
-
akQ
Euclidean triangular symmetry[edit]
-
tH
-
cΔ
-
cH
-
ctH
-
dakH
-
aaaH
-
aaaH, equilateral (close to 3-4-6-12 tiling and 3.4.6.4; 32.4.3.4)
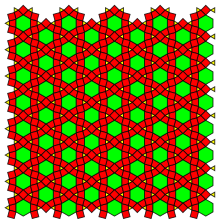
Canonicalization[edit]
| Similar to 3.4.6.4; 324.3.4 | (triangles smaller than midpoint) | Midpoint-connecting 3.4.6.4 | Expanding (3.6)2 |
|---|---|---|---|

|
|

|

|
| Using equilateral triangles (but not regular octagons) |
Midpoint-connecting 4.82 (using regular octagons) |
|---|---|

|

|
Special Tilings (Expand and Ortho)[edit]
Below are the expand and ortho results of a basis of planar tilings: 11 uniform tilings, 4 semiregular tilings, one 4-uniform tiling ('gem' tiling), and one 92-uniform tiling with 14 distinct planigons ('take all' tiling). To expand a uniform tiling, take the midpoints of all regular polygons (ambo), take the midpoints of the resulting regular polygons, take the midpoints of the vertex-figure polygons (in the gaps), and alternate between shrunk regular polygons and shrunk planigons connected by vertices in checkerboard fashion (since e=aa).[2][3] There will be new gap polygons in the expand tilings of lesser significance. This operation tends to form rings around larger regular polygons, with smaller regular polygons acting as ring borders. To ortho a uniform tiling, merely superimpose its dual. Note that '—' stands for elongation, which is not officially a Conway operation.
Note that the canonically expanded triangular and hexagonal tilings are not identical to the rhombitrihexagonal tiling (more appropriately called the rectrihexagonal tiling), but have thin rectangles of ratio instead of (regular) squares.
- ↑ Armstrong, M. A. (Mark Anthony) (1988) Groups and symmetry, Category:New York: Springer-Verlag ISBN: 0387966757. OCLC: 17354658.
- ↑ "Chapter 21: Naming the Archimedean and Catalan polyhedra and Tilings" in (2008) The Symmetries of Things ISBN: 978-1-56881-220-5.
- ↑ Anselm Levskaya. polyHédronisme.