<nowiki>función exponencial natural; természetes exponenciális függvény; funció exponencial natural; Экспонента; natürliche Exponentialfunktion; Fonzion esponenzial; Էքսպոնենտ; 自然指数函数; მაჩვენებლიანი ფუნქცია; 自然指数関数; אקספוננט; functio exponentialis naturalis; экспоненциальная функция; चरघातांकी फलन; Εκθετική συνάρτηση; 자연 지수 함수; Экспоненттік функция; natura eksponenta funkcio; přirozená exponenciální funkce; eksponencijalna funkcija; funzione esponenziale; সূচক ফাংশন; fonction exponentielle naturelle; Експоненциална функция; Экспонента; fungsi eksponen; eksponentfunktsioon; fonsion esponensial; Funcție exponențială; Eksponencijalna funkcija; Espuninziali; função exponencial natural; Експоненцијална функција; eksponentfunkcija; Eksponensiële funksie; eksponentinė funkcija; naravna eksponentna funkcija; Eksponensiyal na punsiyon; função exponencial natural; fungsi eksponensial; ฟังก์ชันเลขชี้กำลัง; eksponentialfunksjon; eksponentialfunksjon; exponentiële functie; படிக்குறிச் சார்பு; eksponencijalna funkcija; اسی دالہ; فانکشنی توانی; natural exponential function; دالة أسية طبيعية; 自然指数函数; Експонента (функція); funzione consistente nell'elemento a potenza della costante di Eulero e; fonction mathématique; показательная функция e^x; Exponentialfunktion zur Basis e; função exponencial com base e; Էքսպոնենտ, տեսողական ֆունկցիա, որտեղ-ն Էյլերի թիվն է։; 以e为底的指数函数; 冪における指数を変数として、その定義域を主に実数の全体へ拡張して定義される初等超越関数; função exponencial com base e; פונקציה מעריכית שהבסיס שלה הוא קבוע אוילר (e); wiskundige functie; विशिष्ट गणितीय कार्य का वर्ग; 以常数e为底的指数函数; دالة أسية ذات الأساس e (أو هـ بالعربية); exponential function with base e, denoted exp(x) or e^x; la unika derivebla funkcio egalanta sian derivaĵon kaj kies valoro ĉe 0 estas 1; jediná funkce, která se rovná své vlastní derivaci a v nule je rovna jedné; functio x ↦ eˣ; función exponencial; exponenciális függvény; funció exponencial; e-Funktion; função exponencial; e^x; exp; 指数函数; 指數函數; 自然指數函數; 指数関数; 自然指数函数; 指数函数; 指数函数; functio exponentialis; הפונקציה המעריכית; natuurlijke exponentiële functie; دالة أسية نيبيرية; دالة الأس النيبيري; دالة الأس الطبيعي; e^x; fonction exponentielle; exponential function; exp; exp(); exp(x); e^x; exp x; 자연지수함수; exp; exp; eksponenta funkcio; e^x; exp; exp(x); exponenciální funkce; экспонента; натуральная экспонента; антилогарифм</nowiki>
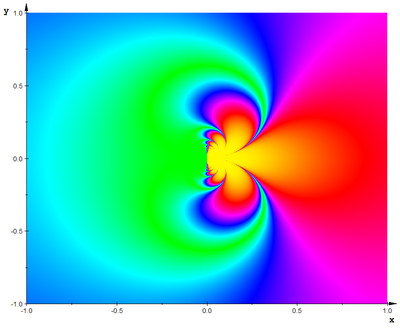
Plots of the Exponential Function over the Complex Plane
[edit]The exponential function is more complicated in the complex plane. On the real axis, the real part follow the expected exponential shape, and the imaginary part is identically zero. However, as the imaginary part changes, the exponential varies sinusoidally, with a period of 2π in the imaginary direction.

In this plot, you can see the main branch on the real axis (y=0), and part of each branch on either side. This plot runs from -2π..2π in the y-direction and from -3..3 in the x-direction.
The colour in the density plot (right) runs from red (large negative values), through green (nearly zero) to blue (large positive values)
Please note that the this colour scheme is non-linear (it is based on the Arctan function and therefore emphaseses changes near zero more), and thus a given change in hue does NOT necessarily reflect a similar change in value, although at the same magnitude, the changes should be identical.
The plot below shows the real part of the exponential function as the operand approaches infinity. This plot is given by:

The plot below shows the absolute value of the real part as the operand approaches infinity:

The colouring of the density plots is different to the graphs above. It runs from green (small), through blue and red to yellow (large). It is highly non-linear and changes near zero give a larger hue shift than large values.

The plot below shows the imaginary part of the exponetial function as the operand approaches infinity. This plot is given by:

Note that the orientation of the surface graph below is different to provide a better view of the structure of the function.
The plot below shows the absolute value of the imaginary part as the operand approaches infinity:

The colouring of the density plots is different to the graphs above. It runs from green (small), through blue and red to yellow (large). It is highly non-linear and changes near zero give a larger hue shift than large values.

The modulus of the value is the same as the value of the exponential of just the real part of the operand. Since the real part behaves as a cosine across the complex plane, and the imaginary part like a sine, the modulus which is related to the real part squared plus the imaginary part squared. As  , it makes sense that the modulus is invariant in the imaginary direction.
, it makes sense that the modulus is invariant in the imaginary direction.

The argument of the exponential function is simply the argument of the operand. The density plot has a linear colour function (an equal change in colour is representative of an equal change in the value of the point). Red is lowest, green is zero and blue is highest.
Taylor Series Approximations
[edit]Real Part, Main Branch
[edit]