Mandelbrot set
Prijeđi na navigaciju
Prijeđi na pretraživanje
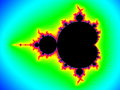
English: The Mandelbrot set, a fractal, named after its creator the French mathematician Benoît Mandelbrot. The set is a map of the Julia set.
Polski: Zbiór Mandelbrota, fraktal, nazwany imieniem francuskiego matematyka. Zbiór ten jest mapą zbiorów Julii.
Slovenščina: Mandelbrotova množica je fraktal, imenovan po avtorju francoskem matematiku Mandelbrotu. Gre za karto Juliajeve množice.
Українська: Множина Мандельброта
-
Benoît Mandelbrot and the set bearing his name
General
[uredi]-
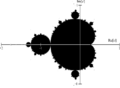
Hi-resolution Mandelbrot set with axes
-
Mandelbrot set and periodicities of orbits
-
Mandelbrot set and colorcoded periodicities of orbits
-
Mandelbrot set with well defined colour stripes
-
Mandelbrot set with irregular colour stripes
-
Mandelbrot set in grayscale
-
Mandelbrot set with smooth color gradient
-
Mandelbrot zoom
-
Inside colour-mapping, (B&W version).
-
Inside colour-mapping, (colour version).
-
Screenshot von RFL Mandelbrot Set Exploration Tool v0.0.4
-
Visualization of Mandelbrot set in complex plane
-
Command-line depiction of the Mandelbrot set.
-
Yet another image of the Mandelbrot Set.
-
Representation of Inner Structure
-
colors
Structure
[uredi]-
Boundaries of hyperbolic components of mandelbrot set
-
Lemniscates - boundaries of level sets of escape time
-
Centers of hyperbolic components
-
All boundaries of level sets of escape time up from n=1
Rays
[uredi]-
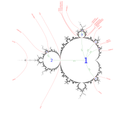
External and internal rays, center and root
-
External rays of Misiurewicz point
-
External ray of Misiurewicz point c=-2
-
Uniformization of complement of Mandelbropt set
-
Wakes near the period 1 continent in the Mandelbrot set
-
Wakes along the main antenna in the Mandelbrot set
Fractalizer
[uredi]Zoom
[uredi]-
Initial image of a zoom sequence with 14 steps
-
Initial image of a corresponding zoom sequence with frames
-
Zoom step 1 of 14
-
Zoom step 1 of 13
-
Zoom step 2 of 14
-
Zoom step 2 of 13
-
Zoom step 3 of 14
-
Zoom step 3 of 13
-
Zoom step 4 of 14
-
Zoom step 4 of 13
-
Zoom step 5 of 14
-
Zoom step 5 of 13
-
Zoom step 6 of 14
-
Zoom step 6 of 13
-
Zoom step 7 of 14
-
Zoom step 7 of 13
-
Zoom step 8 of 14
-
Zoom step 8 of 13
-
Zoom step 9 of 14
-
Zoom step 9 of 13
-
Zoom step 10 of 14
-
Zoom step 10 of 13
-
Zoom step 11 of 14
-
Zoom step 11 of 13
-
Zoom step 12 of 14
-
Zoom step 12 of 13
-
Zoom step 13 of 14
-
Zoom step 13 of 13
-
Zoom step 14 of 14
-
Mandelbrot (Ausschnitt)
-
Mandelbrot (Ausschnitt)
-
Zooming Movie 03
-
Zooming movie 04
-
Zooming movie 06
-
Zooming movie 15
-
High-resolution zoom
-
Featured golden gradient zoom on the Mandelbrot set by more than 31 orders of magnitude.
Iteration
[uredi]-
At a count of 32, the whole image is black, since it is completely inside the false-negative contour.
-
If we allow 64 iterations, some points are no longer falsely inside the set.
-
At 128 iterations, the image is blobby, but recognizable as a fractal.
-
256
-
At 512, we get a nice image. The black dots up and to the left of each "wart" contain tiny cardioids.
-
1024
-
2048
-
Diminishing returns are quite obvious when we use a million iterations. Even with periodicity checking, this one took 10–15 seconds to generate on an Athlon XP 2000+.
-
Number of iterations changing from 1 to 50.
Some details of the Mandelbrot set
[uredi]-
side=0.582; lower-left-point=-0.4+0.5i (made using a JAVA applet archive copy at the Wayback Machine)
-
side=0.0017815; lower-left-point=-0.75+0.06i (made using a JAVA applet archive copy at the Wayback Machine)
-
side=0.004402; lower-left-point=0.28+0.0084i (made using a JAVA applet archive copy at the Wayback Machine)
-
side=0.000191; lower-left-point=-0.78-0.136i (made using a JAVA applet archive copy at the Wayback Machine)
-
side=0.00004; lower-left-point=-1.595+0.000095i (made using a JAVA applet archive copy at the Wayback Machine)
-
side=0.0001558; lower-left-point=-0.75+0.064i (made using a JAVA applet archive copy at the Wayback Machine)
-
side=0.0000829; lower-left-point=0.253-0.0031i (made using a JAVA applet archive copy at the Wayback Machine)
-
side=0.0166; lower-left-point=-1.042-0.0346i (made using a JAVA applet archive copy at the Wayback Machine)
-
center=-0.745-0.1i
-
Calm Mandelbrot, magnified 100,458,337,236 times, 256 iterations
-
Cool Mandelbrot, magnified 248,034,982,258 times, 256 iterations
-
Hot Mandelbrot, magnified 261,880 times, 1024 iterations
-
Galaxy of Galaxies
-
Rendered with a scenery generator
-
Universality of Mandelbrot set
[uredi]-
Mandelbrot sets occurring in the analysis of Newton's method
-
Mandelbrot set occurring in the analysis of Newton's method (detail)
-
Mandelbrot set occurring in the analysis of Newton's method (detail)
-
Mandelbrot set occurring in a model of phase transitions (detail)
-
Mandebrot set embedded in cos(z)+c.
-
Mandebrot set embedded in gaussian exp(-z^2)+c.
Miscellaneous
[uredi]-
Comparing functions, Mandel/Bifurcation.
-
Periodic cycles in the Mandelbrot set
-
Mandelbrot, plane: 1/lambda
-
Relation between Mandelbrot set and en:logistic map
-
Multibrot sets
-
Map of Julia sets showing the resemblance with the Mandelbrot set
-
Mandelbulber v2.23
-
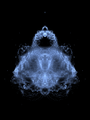
High-resolution Buddhabrot rendering of the Mandelbrot set
First steps in Mandelbrot set
[uredi]-
1.step of Ms
-
2.step of Ms
-
3.step of Ms
-
4.step of Ms
-
5.step of Ms
-
9.step of Ms
-
30.step of Ms
-
part of 30.step of Ms
-
step 1
-
step 2
-
step 3
-
step 4
-
step 5
-
step 6
-
step 7
-
step 8
-
step 9
-
step 10
-
step 11
-
step 12
-
step 13
-
step 14
-
step 15
-
step 16
-
step 17
-
step 18
-
step 19
-
step 20