Category:Kalman filters
algorithm  | |||||
| Upload media | |||||
| Instance of | |||||
|---|---|---|---|---|---|
| Subclass of | |||||
| Named after | |||||
| |||||
 | |||||
Filtre de Kalman : C'est en 1960 que Kalman publie son article révolutionnaire sur "une nouvelle approche du filtrage linéaire". Linéaire : C'est le modèle mathématique qui décrit l'évolution d'un état qui est linéaire en cet état. C'est un modèle linéaire stochastique. Les bruits sont aussi, par hypothèse , tous gaussiens. Le filtre de kalman est optimal: Dans sa théorie, Kalman utilise un critère quadratique qui minimise une énergie, donc très physique. L'énergie qui est minimisée est le carré d'une erreur, en fait la variance de l'erreur d'estimation de l'état du système stochastique. La variance de l'erreur d'estimation est minimale par le filtre de Kalman : C'est içi que réside le caractère optimal du filtre de Kalman.
Le filtre de Kalman est optimal (on ne peut pas trouver un meilleur filtre, la démonstration mathématique est rigoureuse) au sens de l'erreur d'estimation ,en contexte linéaire gaussien.
Media in category "Kalman filters"
The following 13 files are in this category, out of 13 total.
-
-
Basic concept of Kalman filtering.svg 1,701 × 861; 68 KB
-
Exemplo de resultado obtido com o filtro de kalman.svg 769 × 577; 15 KB
-
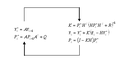
HMM Kalman Filter Derivation.svg 466 × 195; 15 KB
-
HMMKalmanFilterDerivation.png 463 × 239; 7 KB
-
Kalman ex3.PNG 357 × 198; 4 KB
-
Kalman filter model2.svg 534 × 188; 71 KB
-
Kalman Filter.jpg 1,720 × 867; 271 KB
-
Kalman filtresinin temeli.svg 1,499 × 908; 73 KB
-
Kalman Polynom Test.svg 450 × 315; 111 KB
-
Kalman Polynom vs GLS.svg 540 × 288; 44 KB
-
Kalman-filter en.svg 899 × 513; 194 KB
-
Simulink radar detect aircraft.png 1,367 × 423; 79 KB
