Coriolis effect
apparent or fictitious force on objects moving within a reference frame that rotates with respect to an inertial frame | |||||
| Upload media | |||||
| Pronunciation audio | |||||
|---|---|---|---|---|---|
| Subclass of |
| ||||
| Named after | |||||
| Discoverer or inventor | |||||
| Time of discovery or invention |
| ||||
| Different from | |||||
| |||||
 |
The Earth is rotating, and therefore it is an oblate spheroid (like a football with flattned ends). The vector representing true gravity can be decomposed in a component perpendicular to the surface and a component perpendicular to the Earth's axis. The component of true gravity that acts perpendicular to the Earth's axis provides the force that keeps objects at the same latitude.
In the hypothetical case of a perfectly spherical rotating celestial body, all water and air would gather at the equator. Each component of true gravity has a different effect: the effect of the perpendicular to the surface component is that objects remain tightly on Earth; the effect of the perpendicular to the Earth's axis component is that all objects that are stationary with respect to the Earth remain on the same latitude, rather than sliding to the equator. The arrow on the outside shows the local direction of a plumb line; the line that is perpendicular to the surface. | ||
 |
The Earth has taken a shape such that the direction of the gravitational force is slightly tilted to the Earth surface. The equatorial component of this force
counteracts the "centrifugal force" preventing air and water to slip towards the equator. In case of a wind in eastward direction the centrifugal force of the atmosphere is stronger and a slip towards the equator is initiated. In case of a wind in westward direction the centrifugal force of the atmosphere is weaker and a slip away from the equator is initiated. This is the "coriolis effect" for east/west winds | ||
 |
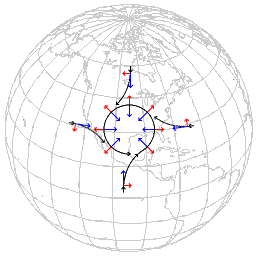
Due to the coriolis effect the wind direction turns right in the northern hemisphere and left in the southern hemisphere resulting in spiral. The reason for an east/west wind to turn is explained in the figure above. The reason for a north/south wind to turn is simply the difference in eastward velocity of the ground at different latitudes. The detailed mathematics of this can be found in
https://wgpqqror.homepage.t-online.de/coriolis.pdf archive copy at the Wayback Machine | ||
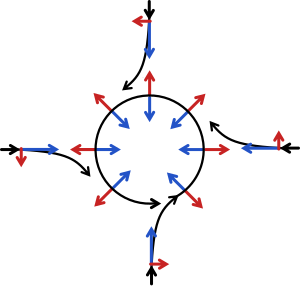  |
Schematic representation of flow around a low pressure area. Pressure gradient force represented by blue arrows, The Coriolis effect tendency, always perpendicular to the velocity, by red arrows. | ||
 |
Parabolic shape formed by the surface of a liquid under rotation. | ||
 |
Schematic representation of harmonic oscillation on parabolic surface. The concavity is exaggerated. This animation offers a sideview of what happens in the next animation (Image:Coriolis_effect06.gif). | ||
 |
Schematic representation of a puck moving over a parabolical surface.
When the centripetal force causes the puck to move closer to the center of attraction the centripetal force is accelerating the puck, so the angular velocity of the puck increases. This is an example of the coriolis effect.  | ||
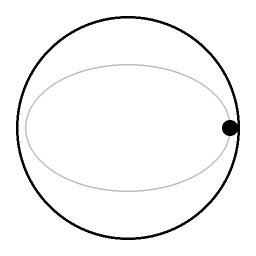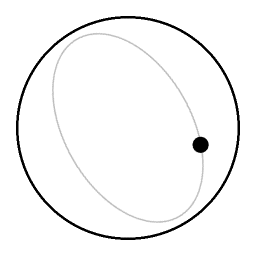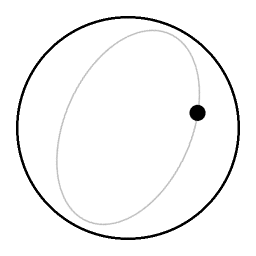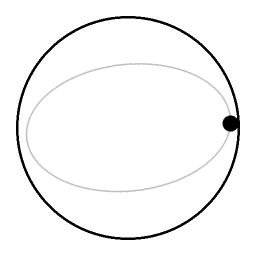 |
the elliptical trajectory of the preceding animation as seen by a videocamera that is co-rotating with the turntable.
Due to the coriolis effect demonstrated in the preceding animation (Image:Coriolis_effect06.gif), the angular velocity of the puck is changing continuously. As seen from a rotating point of view there is an apparent motion along a small circle. | ||
 |
The parametric equation is as follows:
This can also be written as follows, showing that the elliptical motion with that particular velocity profile can be seen as a vector addition of two uniform circular motions: To be used in conjunction with the animations Image:Coriolis_effect06.gif and Image:Coriolis_effect.07.gif. | ||
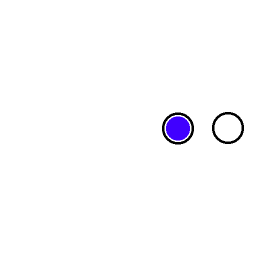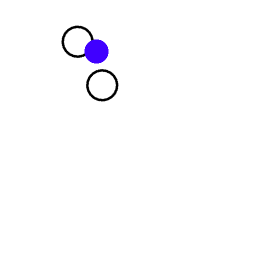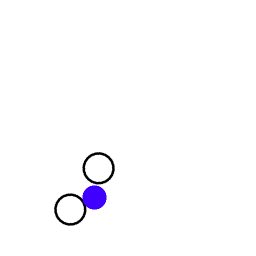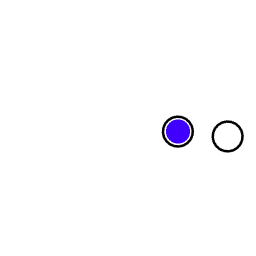 |
The blue dot is an object that is being thrown back and forth from the inner platform to the outer platform. During the flight there is no force acting on the object, so it moves in a straight line, the target is moving along a curvilinear trajectory. | ||
 |
This image presents a hypothetical situation. If masses of air can flow without meeting any resistance, how will they flow? Due to the shape of the Earth, the motion will tend to follow so-called inertial circles. These circles correspond to what is shown in Image:Coriolis_effect07.gif and in Image:Mass point affected by coriolis.svg |  |
Schematic, simplified representation of atmospheric inertial oscillation as seen from a non-rotating point of view. The black globe represents a weather balloon being swept along with inertial wind. Inertial wind is the name for the wind pattern that can occur in the absence of a pressure gradient.
With friction very small, inertial wind is a form of frictionless motion over the surface of an oblate spheriod. The Earth is an oblate spheroid, because it is rotating. The vertical circles are not meridians. One full cycle of the animation corresponds to 24 hours. When the air mass is moving nearer to the pole it is picking up speed. Furthest away from the poles the velocity is slowest (flowing east to west with respect to the Earth). The velocity with respect to the Earth is close to constant, the direction with respect to the Earth is continuously changing to the left. To be used in conjunction with the image Image:Coriolis_effect14.png |
 |
Visualisation of the coriolis effect.
In the inertial frame of reference (upper part of the picture), the black object moves in a straight line. However, the observer (red dot) who is standing in the rotating frame of reference (lower part of the picture) sees the object as following a curved path. | ||
|
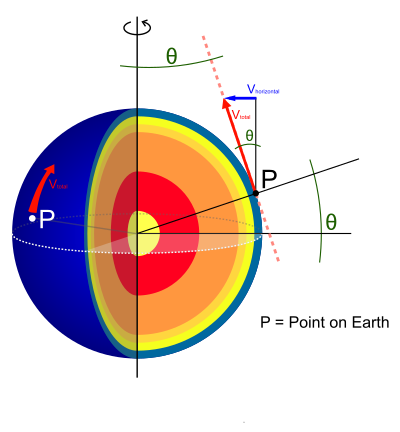
How the coriolis effects work
The red line is an object on earth travelling from point P at the speed (V_total). For the coriolis effect only the horizontal speed (V_horizontal) is of importance. To get from one can say: The coriolis force is: |








