Julia set

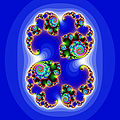
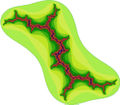
English: The Julia set is a fractal. It was first created by the French mathematician Gaston Julia. The set was then long forgotten until Benoît Mandelbrot (who was taught by Julia in the 40s), made a work about it in the early 1980s. See also: Mandelbrot set.

Slovenščina: Juliajeva množica je fraktal. Prvi ga je opisal francoski matematik Gaston Julia. Množica je nato dolgo časa ostala pozabljena, dokler ni o njej v zgodnjih 1980-ih napisal knjige (Juliajev učenec v 40-ih). Glejte tudi: Mandelbrotova množica.

Polski: Zbiór Julii to fraktal. Pierwszy opisał i stworzył go francuski matematyk Gaston Julia. Zobacz też: Zbiór Mandelbrota.

• 
  Julia-Menge
• 
  From the escape-time function
• 
  Special colour-mapping
• 
  Detail of centerpart
• 
  Detail of centerpart
• 
  Highres image
• 
  Highres image
• 
  From the reversed formula.
• 
  From the reversed formula.
• 
  From the reversed formula.
• 
  From the reversed formula.
• 
  Quaternion set, (4D).
• 
  From the reversed formula.
• 
• 
• 
• 
• 
• 
  Time escape Julia set from coordinate (phi-2, phi-1)
• 
  Time escape Julia set from coordinate (1-phi, 0)
• 
  Time escape Julia set from coordinate (-0.297491, -0.641051)
• 
  Image:Time escape Julia set from coordinate (0.285, 0)
• 
• 
• 
  Julia set for c=i made with IIM
• 
  Julia Set using z = z^2 + c, where c = -0.8+0.156i
• 
  Julia Set using z = z^10 + c where c = -0.925 + 0.19i
• 
  Julia Set using z = z^12 + c where c = -0.89511414 + 0.1i
• 
  Level curves of escape time
• 
  Filled-in Julia set
• 
  Binary decomposition of basin of attraction of infinity and finite attractor
• 
  Modified IIM
• 
  Fatou components
• 
  Modified IIM and critical orbit
• 
  Julia set of a cubic polynomial
• 
  z→z²-0.742+0.1i
• 
  Inner Structure of Julias: Cell-like
• 
  Inner Structure of Julias: Binary Fractal
• 
  Inner Structure of Julias: Similarity and Distortion
• 
  Inner Structure of Julias: Cell clusters
• 
  Inner Structure of Julias: Braids
• 
  Inner Structure of Julias: Coccid

Map of Julia sets

• 
• 
  Map of the set.
• 
  Julia set for values of c ranging from -2.2-1.2i to 0.6+1.2i

3D

• 
  3D slice of a 4D Quaternion set
• 
• 
• 
• 
• 
• 
• 
• 
• 
• 

Animations

• 
  animated zoom of z→z²+c for fixed c
• 
  Julia set fractal animation
• 
  JUlia set (white) for z→z²+c as c changes
• Animated 3D slice of a 4D Quaternion set

Miscellaneous

• 
  a scenery render of a julia set.
• 
  Julia Set in Mandel: Fatou set
• 
  Julia set in Mandel: Structure, see above
• 
  Description of the dynamics inside the Douady's rabbit.