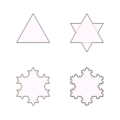
Koch snowflake
Jump to navigation
Jump to search
English: The Koch snowflake (or Koch star) is a mathematical curve and one of the earliest fractal curves to have been described.
Deutsch: Wenn man den Ersetzungsprozess der Koch-Kurve nicht mit einer Strecke, sondern mit einem gleichseitigen Dreieck durchführt, erhält man die kochsche Schneeflocke.
Français : Le flocon de Koch est une construction de courbes planes et l'une des premières fractales à avoir été décrite.
fractal and mathematical curve | |||||
| Upload media | |||||
| Instance of |
| ||||
|---|---|---|---|---|---|
| Named after | |||||
| Discoverer or inventor | |||||
| Time of discovery or invention |
| ||||
| Different from | |||||
| |||||
Illustrations[edit]
Iteration[edit]
-
Snowflake, 0th iteration
-
Snowflake, 1st iteration
-
Snowflake, 2nd iteration
-
Snowflake, 3rd iteration
-
Snowflake, 4th iteration
-
Snowflake, 5th iteration
-
Snowflake, 6th iteration
-
Snowflake, 7th iteration
Animations[edit]
Scripts[edit]
Programs that produce representations of the fractal in various languages.
Logo[edit]
Below is a recursive implementation in Logo. It can be tried out with most implementations of Logo, or online with the Java implementation XLogo.
Try start, call rt 30 koch 100.
to koch :x repeat 3 [triline :x rt 120] end to triline :x ifelse :x < 1 [fd :x] [triline :x/3 lt 60 triline :x/3 rt 120 triline :x/3 lt 60 triline :x/3] end
Web Turtle[edit]
Here follows a sample implementation of the Koch curve for a Turtle robot written in a Logo-like language. It can be tried out online with Web Turtle. Change the value of A in the first line to any number from 1 to 5 to see the different levels of complexity.
LET A 5 ; calculate adjusted side-length LET B 243 REPEAT A LET B B/3 NEXT ; place pointer POINT 150 MOVE 140 POINT 0 ; start GO SIDE RIGHT 120 GO SIDE RIGHT 120 GO SIDE ; finished. END ; main loop # SIDE GO F LEFT 60 GO F RIGHT 120 GO F LEFT 60 GO F RETURN ; forward # F IF A > 1 ; go deeper depending on level LET A A-1 GO SIDE LET A A+1 ELSE ; or just do a single line DRAW B ENDIF RETURN
Python[edit]
Here is the Koch curve in Python 3.1.
import turtle
koch_set = "F"
iterations = 5
for i in range(iterations):
koch_set = koch_set.replace("F","FLFRFLF")
turtle.down()
for move in koch_set:
if move == "F":
turtle.forward(100.0 / (3 ** (iterations - 1)))
elif move == "L":
turtle.left(60)
elif move == "R":
turtle.right(120)
The program can be easily modified to show the entire snowflake:
import turtle
koch_flake = "FRFRF"
iterations = 5
for i in range(iterations):
koch_flake = koch_flake.replace("F","FLFRFLF")
turtle.down()
for move in koch_flake:
if move == "F":
turtle.forward(100.0 / (3 ** (iterations - 1)))
elif move == "L":
turtle.left(60)
elif move == "R":
turtle.right(120)
Flash ActionScript 3[edit]
The source for a Koch Snowflake in Flash AS3:
var sideLength:Number = 400
var down:Number = (sideLength/2) * Math.tan(Math.PI/6)
var up:Number = (sideLength/2) * Math.tan(Math.PI/3) - down
var p1:Point = new Point(-sideLength/2,down);
var p2:Point = new Point(sideLength/2,down);
var p3:Point = new Point(0,-up);
var p4:Point = new Point();
var p5:Point = new Point();
var rot:Number = 0
var lines:Array = [p1,p2,p3]
var tempLines:Array = []
for(var iterations:uint = 1; iterations <= 9;iterations++){
sideLength /= 3
for(var loop:uint = 0; loop <= lines.length - 1; loop++){
p1 = lines[loop]
p2 = lines[loop+1]
if(loop == lines.length-1){p2 = lines[0]}
rot = Math.atan2(p2.y - p1.y, p2.x - p1.x)
p3 = p1.add(Point.polar(sideLength,rot))
rot += Math.PI/3
p4 = p3.add(Point.polar(sideLength,rot))
rot -= 2*Math.PI/3
p5 = p4.add(Point.polar(sideLength,rot))
tempLines.push(p1)
tempLines.push(p3)
tempLines.push(p4)
tempLines.push(p5)
}
lines = tempLines
tempLines = []
}
lines.push(p2)
var line:Sprite = new Sprite()
addChild(line)
line.graphics.lineStyle(0,0x000000)
line.graphics.moveTo(lines[0].x,lines[0].y)
trace(lines.length)
for(var a:uint = 0; a<lines.length;a++){
line.graphics.lineTo(lines[a].x,lines[a].y)
}
stage.addEventListener(MouseEvent.MOUSE_DOWN, mouseDown)
function mouseDown(event:MouseEvent):void {line.startDrag()}
stage.addEventListener(MouseEvent.MOUSE_UP, mouseReleased);
function mouseReleased(event:MouseEvent):void {line.stopDrag()}
See also: Koch curve