Schulze method
Jump to navigation
Jump to search
The Schulze method is a voting system developed in 1997 by Markus Schulze that selects a single winner using votes that express preferences. The method can also be used to create a sorted list of winners. The Schulze method is also known as Schwartz Sequential Dropping (SSD), Cloneproof Schwartz Sequential Dropping (CSSD), Beatpath Method, Beatpath Winner, Path Voting, and Path Winner.
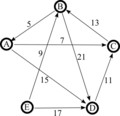
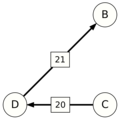
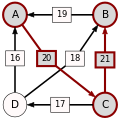
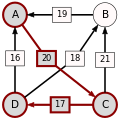
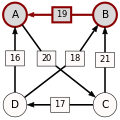
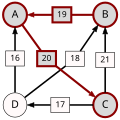
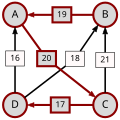
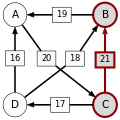
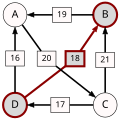
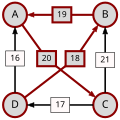
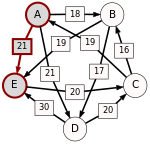
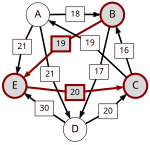
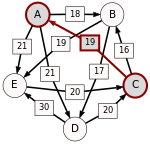
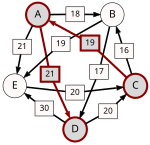
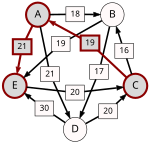
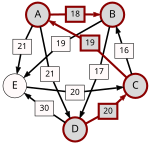
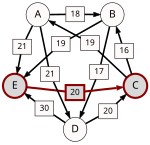
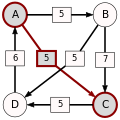
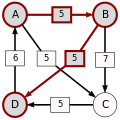
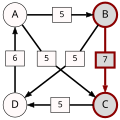
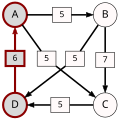
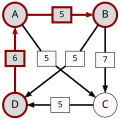
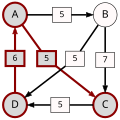
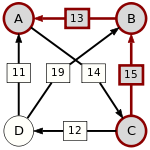
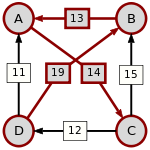
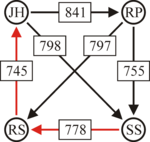
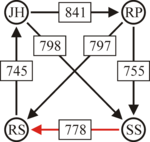
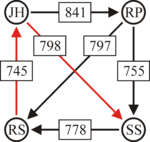
An example for the "Cloneproof Schwartz Sequential Dropping" heuristic for the Schulze method:
Sequence in SVG:
Same content in PNG:
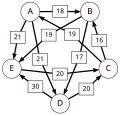
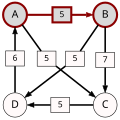
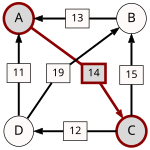
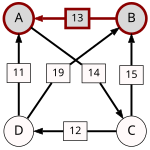
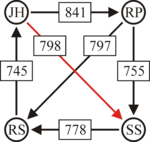
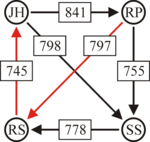
Another example for the "Cloneproof Schwartz Sequential Dropping" heuristic for the Schulze method:
Sequence in SVG:
Same content in PNG:
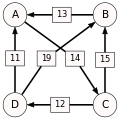
Other examples for the Schulze method:
Sequence in SVG:
Same content in PNG:
Pamphlets: