Category:Gamma and related functions
Jump to navigation
Jump to search
extension of the factorial function, with its argument shifted down by 1, to real and complex numbers | |||||
| Upload media | |||||
| Instance of |
| ||||
|---|---|---|---|---|---|
| Discoverer or inventor |
| ||||
| Different from | |||||
| |||||
Splitting the Gamma function The Gamma function can be split in to two functions, for real r, -∞ < r < +∞,
Γ(r) = e^(-1)*Y(r) + E(r) where Y(r+1) = r*Y(r)+1 with Y(0) ≈ 0.59634 73623, and
E(r)=∑_(m=0)^∞▒〖(-1)^m/((r+m)*m!).〗
Ref: Stephens C. (TWRI Policy and Research) (2022). Splitting the Gamma function see:
http://www.twri.org.uk/sites/default/files/twri/splitgamma_1.pdf
Subcategories
This category has the following 7 subcategories, out of 7 total.
C
E
- Euler beta function (4 F)
- Exponential integral (11 F)
F
I
- Incomplete gamma function (3 F)
P
S
- Stirling's approximation (19 F)
Media in category "Gamma and related functions"
The following 33 files are in this category, out of 33 total.
-
Desmos Complex Function.jpg 1,520 × 1,326; 376 KB
-
Factorial Interpolation.svg 720 × 540; 33 KB
-
Factorial plot.png 640 × 480; 14 KB
-
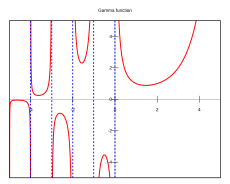
Gamma function 2.png 420 × 270; 10 KB
-
Gamma function.png 440 × 680; 8 KB
-
Gamma function.svg 468 × 466; 28 KB
-
Gamma plot pl.gif 818 × 557; 17 KB
-
Gamma plot points marked.svg 600 × 480; 21 KB
-
Gamma plot real.png 1,200 × 1,000; 53 KB
-
Gamma plot zh.svg 600 × 480; 15 KB
-
Gamma plot-lv.svg 600 × 480; 14 KB
-
Gamma plot.svg 600 × 480; 13 KB
-
Gamma property.gif 600 × 250; 719 KB
-
Gamma+1.png 524 × 478; 33 KB
-
Gamma-function.svg 440 × 440; 16 KB
-
Gamma.png 484 × 484; 14 KB
-
Gammafunktion.svg 567 × 567; 35 KB
-
Generalized factorial function more infos.svg 500 × 315; 54 KB
-
Generalized factorial function.svg 500 × 315; 42 KB
-
Inverse Gamma function with branches.svg 472 × 600; 12 KB
-
Inverse of Gamma function.svg 377 × 243; 10 KB
-
Log gamma absolute.png 996 × 992; 207 KB
-
Log gamma imag.png 996 × 992; 197 KB
-
Log gamma real.png 996 × 992; 174 KB
-
Mplwp gamma positive.svg 600 × 400; 20 KB
-
Mplwp gamma.svg 600 × 400; 30 KB
-
Mplwp one over gamma.svg 600 × 400; 29 KB
-
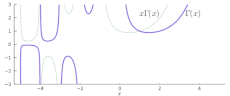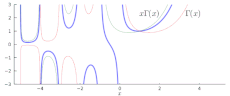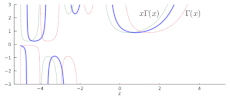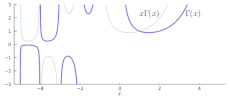
Pochhammer.svg 359 × 224; 69 KB
-
Rgamma plot real.png 1,200 × 1,000; 46 KB
-
Rgamma plot real.svg 540 × 360; 19 KB
-
Todiste61.png 523 × 655; 14 KB
-
Upper incomplete gamma function.jpg 1,192 × 682; 74 KB
-
X to the power of x and x factorial.png 116 × 465; 8 KB