Set theory
Jump to navigation
Jump to search
English: Set theory is a branch of Mathematics.
It's regarded the foundation of mathematics, and closely related with logic.
It's regarded the foundation of mathematics, and closely related with logic.
Operations on and relations between two sets
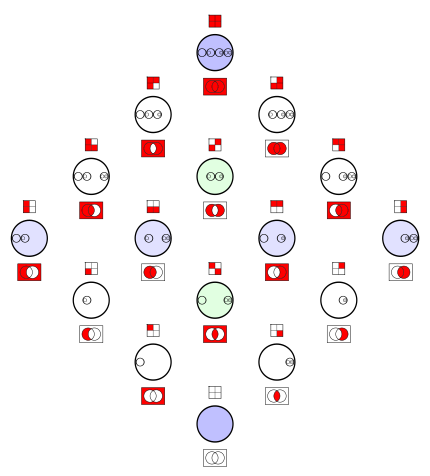
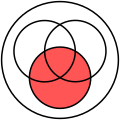
[edit]The Venn diagrams in the left matrix represent set operations - e.g. the intersection ![]() ,
,
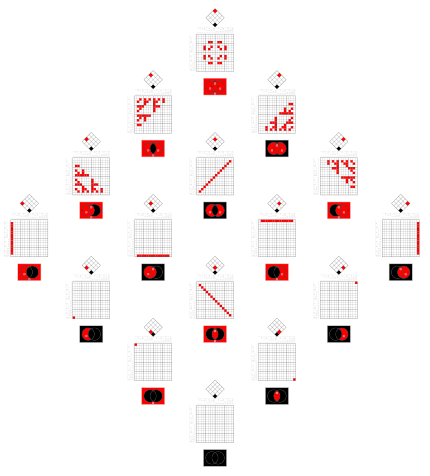
those in the right matrix represent set relations - e.g. the subset relation ![]() , more usually represented by an Euler diagram:
, more usually represented by an Euler diagram: ![]()
The set theoretic descriptions are over the Venn diagrams:
| ∅c |
A = A |
|||||||||||||
| Ac Bc |
true A ↔ A |
A B |
A Bc |
AA |
A Bc |
|||||||||
| A Bc |
¬A ¬B A → ¬B |
A B |
A B A ← ¬B |
Ac B |
A B |
A¬B |
A = Bc |
A¬B |
A B |
|||||
| Bc |
A ¬B A ← B |
A |
A B A ↔ ¬B |
Ac |
¬A B A → B |
B |
B = ∅ |
AB |
A = ∅c |
A¬B |
A = ∅ |
AB |
B = ∅c | |
| ¬B |
A Bc |
A |
(A B)c |
¬A |
Ac B |
B |
Bfalse |
Atrue |
A = B |
Afalse |
Btrue | |||
| A ¬B |
Ac Bc |
A B |
A B |
¬A B |
AB |
|||||||||
| ¬A ¬B |
∅ |
A B |
A = Ac |
|||||||||||
| false A ↔ ¬A |
A¬A |
|||||||||||||
| These sets (statements) have complements (negations). They are in the opposite position within this matrix. |
These relations are statements, and have negations. They are shown in a separate matrix in the box below. | |||||||||||||
| more relations | ||||
|---|---|---|---|---|
|
Syllogisms
[edit]Syllogisms can be described in the language of set theory.
| 1 |  Barbara |
 Barbari |
 Darii |
 Ferio |
 Celaront |
 Celarent |
||||||||
| 2 |  Festino |
 Cesaro |
 Cesare |
 Camestres |
 Camestros |
 Baroco |
||||||||
| 3 |  Darapti |
 Datisi |
 Disamis |
 Felapton |
 Ferison |
 Bocardo | ||||||||
| 4 |  Bamalip |
 Dimatis |
 Fesapo |
 Fresison |
 Calemes |
 Calemos |

Partitions
[edit]Various files
[edit]-
Venn 0101 0101.svg
-
Venn 0011 0011.svg
-
Venn 0000 1111.svg
-
Venn 0000 0001.svg
All 256 Venn diagrams of this kind can be found here